Nom du chapitre : Repérage et vecteurs (Chap 2)
Objectifs :
- Interpréter et déterminer graphiquement les coordonnées d’un vecteur
- Calculer les coordonnes d’un vecteur
- Calculer la distance entre deux points A et B connaissant les coordonnées du vecteur
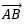
Prérequis :
- Identifier et décrire une translation ; comprendre son effet sur une figure
- Repérer un point du plan par ses coordonnées dans un repère choisi
- Utiliser le théorème de Pythagore pour calculer des longueurs
Énoncé élève :
Problème 1 / Document émetteur
Une équipe de 3 scientifiques a mené une étude durant 20 jours en océan Arctique.
Cette équipe a été déposée sur un morceau de banquise d’environ 800m de longueur, puis elle s’est laissée dériver avec la banquise. L’épaisseur de la glace permettait en effet de s’installer en sécurité durant plusieurs semaines.
La figure suivante montre la position du morceau de glace relevée 4 jours consécutifs à 12h00 GMT entre le lundi et le jeudi.
Le point A désigne la position choisie par les scientifiques pour installer le camp le 1er jour.
- La position du camp le lundi est connue. Ecrivez un message permettant à un autre groupe de positionner sur une carte ce même camp les mardi ; mercredi et jeudi suivants.
- Les scientifiques estiment avoir dérivé sur environ 16 km, qu’en pensez-vous ?
Problème 1 / Document récepteur 1
Problème 1 / Document récepteur 2
Organisation pratique : Cet exercice est un jeu de communication couplé avec une activité autonome de recherche.
La classe est partagée en deux groupes l’un qualifié de groupe 1 émetteur et l’autre de groupe 2 récepteur
1/ Le professeur présente les deux activités qui seront menées conjointement :
A/ un jeu de communication pour lequel le groupe émetteur a pour tâche d’écrire un message le plus explicite possible à destination des récepteurs qui dans un deuxième temps devront utiliser ce message pour réaliser une tâche simple.
B/ une activité de recherche autonome intitulée « pavage du Caire » que tous les élèves devront à leur tour réaliser.
2/ Le professeur distribue le document émetteur au groupe 1 et l’activité « pavage du Caire » au groupe 2
3/ Après 15 min de travail, le professeur récolte les messages qu’il distribue au groupe 2 et remet au roupe 1 l’activité « pavage du Caire »
4/ 15 min plus tard, les productions du groupe 2 sur l’activité « banquise » sont ramassées et font l’objet d’une synthèse collective. (L’usage d’un visualiseur est ici fortement conseillé pour l’affichage de quelques productions choisies en parallèle des messages correspondants)
Commentaires : Il semble opportun durant la mise en commun d’exhiber les productions correctes en lien avec des messages clairs et sans ambiguïté ainsi que des productions erronées liées soit à une mauvaise interprétation du message soit à des messages incomplets ou erronés (utilisation de coordonnées de points sans précision du repère choisi ; non prise en compte de l’orientation indiquée par la rose des vents…).
Un point sur la distance totale parcourue par le bloc de glace permettra d’établir la formule de calcul de la distance AB en fonction des coordonnées du vecteur
Remarque 1 : Selon la nature des messages produits, cette activité pourra aussi être l’occasion d’établir un procédé de calcul des coordonnées d’un vecteur en fonction des cordonnées de ces extrémités.
Remarque 2 : La formule 
semble à ce stade plus facile à mémoriser et à utiliser par l’élève (en référence directe avec le théorème de Pythagore) que la formule « usuelle »
Activité annexe « Pavage du Caire » / document élève
En géométrie, le pavage du Caire est un pavage du plan constitué de pentagones irréguliers. Il porte ce nom car il apparait dans les rues du Caire, en Égypte, ainsi que dans l’art musulman.
La pièce de base un pentagone convexe ABCC’B’ ayant les caractéristiques suivantes : ses 5 côtés ont même longueur ; il possède un axe de symétrie et 2 de ses angles sont droits.
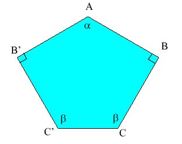
Décrire l’ensemble des transformations permettant de recouvrir entièrement le plan à l’aide de cette unique pièce de base.
