Sur la figure ci-contre,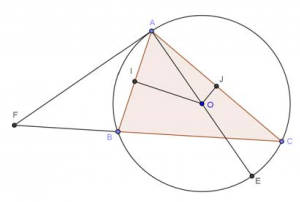
ABC est un triangle quelconque inscrit dans le cercle Γ de centre O tel que :
- la tangente en A au cercle Γ coupe la droite (BC) en F ;
- le point E diamétralement opposé au point A sur le cercle Γ est distinct de B et C ;
- les points I et J sont les milieux respectifs des segments [AB] et [AC].
- Citer les triangles isocèles que l’on peut former à l’aide des points de la figure.
- Justifier que les triangles FAO et AIO sont rectangles.
- La droite (OI) coupe la droite (AF) en G.
On considère la symétrie s d’axe (OI). Compléter le tableau :
| image par s | |
| A | |
| O | |
| G | |
| (AO) | |
| (AG) |
Montrer que la droite (BG) est tangente au cercle Γ.
Des points qui appartiennent à un même cercle sont dits cocycliques. Justifier que les points A, I, O et J sont cocycliques.


