Le regard et la pensée géométrique évoluent peu à peu avec la scolarité de l’enfant, passant de la géométrie perceptive, liée aux objets réels, aux cycles 1 et 2, à la géométrie du raisonnement (ou géométrie théorique) au collège.
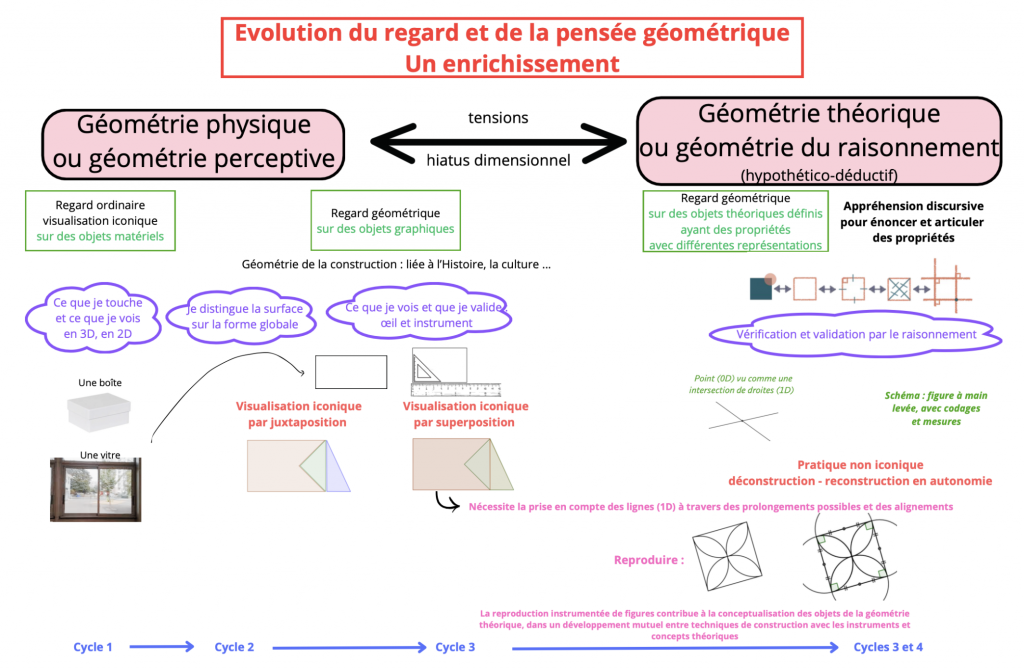
La classe de 6ème est une étape charnière dans cette évolution, pendant laquelle on apprend à ne pas croire ce que l’on voit, à raisonner sur des figures abstraites dont on ne fait que des représentations sous forme de schémas codés, à reconnaître, par exemple, un rectangle dans des situations très différentes. Et pourtant, la géométrie liée à la réalité, aux objets et aux instruments n’est jamais abandonnée. Ces différentes formes de géométrie se complètent et s’enrichissent mutuellement.
Ainsi, comme on peut le lire dans le fascicule « Résolution de problèmes au collège », « En géométrie, les élèves peuvent rencontrer deux types de difficultés liées à la perception : penser ce qui n’est pas visible (en particulier en géométrie dans l’espace), et penser juste même lorsque le visible induit en erreur (figures à main levée erronées en géométrie plane par exemple) » (page 156).
La lecture de schémas codés en 6ème
Exemple d’exercice :
Étape 1 : figures a, b et c.
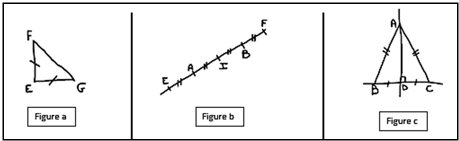
Dans un premier temps, on peut guider les élèves en leur posant des questions ciblées, comme « que peut-on dire du point A par rapport au segment [EI] dans la figure b ? », voire fermées « Pourquoi la droite (AD) est-elle la médiatrice du segment [BC] dans la figure c ? », sachant que les élèves peuvent utiliser ici aussi bien la définition de la médiatrice d’un segment (droite coupant le segment perpendiculairement et en son milieu) ou sa propriété caractéristique (ensemble des points équidistants des extrémités du segment), mais on les amène à choisir entre les deux, sans faire la liste exhaustive de tout ce qu’ils voient et peuvent utiliser comme codages.
Rappel : en mathématiques, une propriété caractéristique est une propriété que possède l’objet considéré (et déjà défini), et que possèdent seulement les objets identiques à lui. Elle permet ainsi de caractériser, de redéfinir, l’objet. Elle doit être énoncée clairement dans les deux sens logiques, direct et réciproque.
Dans un second temps, des figures proches des figures a, b et c pourraient être données avec une consigne plus ouverte : « Quelles informations vous donnent ces figures ? » ou « Quelles égalités de longueur pouvez-vous écrire ? ». Les figures d, e et f peuvent alors être utilisées avec une consigne ouverte, par exemple « pour chacune des figures, après avoir fait la liste de tous les éléments géométriques connus, indiquer les propriétés que l’on peut en déduire, voire les natures exactes des quadrilatères ». On invite ainsi les élèves à prendre le temps de lire les codages et éléments de texte joints, puis à établir des propriétés de ces figures. On pourra les aider en leur demandant si le quadrilatère d est un trapèze, si le point L est le centre du grand cercle passant par A et M, ou si le quadrilatère JOLI est un carré. Ces réponses devront être justifiées oralement.

En fin de 6ème, on attend que la lecture et la compréhension des figures a, b et c soit automatisée, sinon un travail spécifique devra être mené avec les élèves qui en ont besoin pendant que les autres travailleront sur des figures plus complexes.
Inversement, on pourra mener un travail répété dans l’année sur la traduction d’un texte décrivant une figure en un schéma codé qui servira, par la suite, de support au raisonnement (voir article ou partie Représenter et observer les figures pour raisonner en 6e).
Découvrir une propriété sans la démontrer
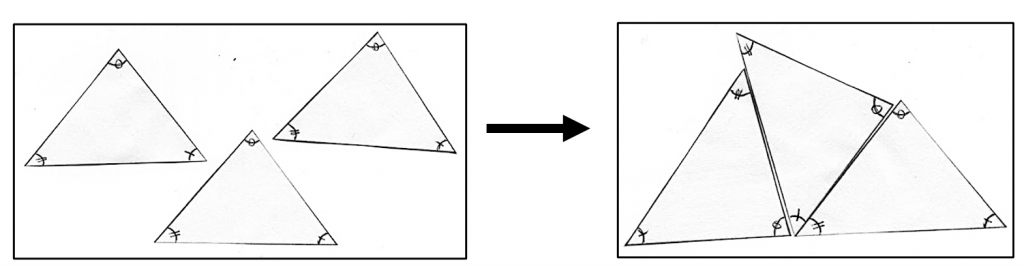
Dans le travail sur les angles et les triangles, qui sont des parties importantes du nouveau programme de 6ème (2025), l’élève doit apprendre que la somme des angles d’un triangle est égale à 180°. Or sans la connaissance de la symétrie centrale, il n’est pas possible de démontrer cette propriété. On reste donc d’abord sur une géométrie perceptive et une géométrie des instruments pour établir ce résultat. On peut donner un triangle différent à tous les élèves et leur demander de mesurer les trois angles au rapporteur puis de les ajouter. Chaque élève va obtenir une somme proche de 180°, mais qui souvent ne sera pas 180° : en effet, les mesures d’angles sont souvent imprécises en raison de la difficulté de manipulation, notamment pour les triangles les plus petits pour lesquels il aura fallu prolonger les côtés (on pourra ainsi donner aux élèves les plus minutieux et soigneux les figures les plus petites). L’usage du logiciel Geogebra par le professeur permet ensuite d’affiner la conjecture (raisonnement inductif) : en déplaçant les sommets du triangle construit, on explique aux élèves qu’on fait apparaître une très grande quantité de triangles différents. Pourtant la somme des angles que l’on aura affichée restera inchangée. Ce raisonnement inductif conduit à l’élaboration d’une conjecture, que l’on formulera avec « si … alors … » pour faire apparaître le sens logique. Par exemple, « si une figure est un triangle, alors la somme de ses angles est égale à 180° » (des reformulations sans le mot somme seront utiles ensuite pour nombre d’élèves). Le professeur doit ensuite expliquer que ce résultat doit être prouvé, qu’il ne dépend pas de lui, d’eux, ni des exemples qu’il a donnés sur papier ou qu’il a fait apparaître sur Geogebra, mais qu’il est vrai dans tout l’univers. Les connaissances de 5ème permettront de le prouver et en 6e, on mentionnera que cette propriété est admise. Une activité de découpage et manipulation de triangles dont les trois angles ont été marqués différemment permet, comme le préconise le document « exemples de mise en œuvre – 6e », de s’appuyer « sur l’accolement de [trois] triangles identiques pour constater que la somme des angles d’un triangle est un angle plat avant d’admettre ce résultat ». Pour cette activité, on utilisera le vocabulaire « somme des trois angles adjacents », le terme « supplémentaires » étant réservé à deux angles. Vigilance : il peut être difficile pour des élèves de transférer le résultat de la somme des trois angles accolés, chacun appartenant à un triangle différent, à celle des trois angles d’un seul triangle.
Par la suite, le résultat devra être mémorisé puis il pourra être utilisé pour calculer la mesure d’un angle dans un triangle schématisé dont on connaît les mesures des deux autres angles, puis pour des calculs un peu plus complexes (voir article ou partie Raisonner en géométrie en 6e)
D’autres résultats doivent être admis en 6e, peu d’éléments pouvant être démontrés par les élèves ou même par le professeur, en particulier :
- Domaine des nombres et calculs : le nombre 𝜋 ne peut pas s’écrire sous la forme d’une fraction.
- Domaine des grandeurs et mesures : pour tous les disques, le rapport entre leur périmètre et leur diamètre est un nombre constant noté π.
- le plus court chemin pour aller de A à B est le segment [AB]
- la médiatrice d’un segment est un axe de symétrie de ce segment
- si un point est à égale distance des extrémités d’un segment, alors il appartient à la médiatrice de ce segment (la réciproque de cette propriété peut être prouvée une fois donnée la définition de la symétrie axiale et admise la propriété de conservation des distances par symétrie. La propriété directe et sa réciproque forment alors la propriété caractéristique de la médiatrice d’un segment).
- deux angles opposés par le sommet sont de même mesure
- la bissectrice d’un angle est l’axe de symétrie de cet angle.
- la conservation des distances par une symétrie axiale
- la conservation des angles par une symétrie axiale.
Les définitions suivantes seront découvertes grâce à des activités spécifiques :
- le cercle de centre O et de rayon 2 cm est l’ensemble des points situés à 2 cm de O
- le disque de centre O et de rayon 2 cm est l’ensemble des points dont la distance à O est inférieure ou égale à 2 cm
Baisser la charge cognitive
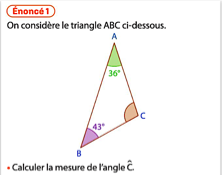
L’énoncé suivant, trouvé dans le manuel Transmath 6e (2025), peut poser plusieurs difficultés aux élèves :
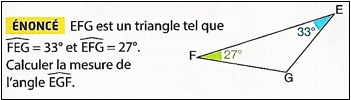
En effet, les mêmes indications sont données dans le texte et sur la figure, ce qui peut ralentir certains élèves qui vont chercher à faire le lien entre elles, voire à les vérifier. Bien sûr, si dans un premier temps, on peut diminuer la charge cognitive des élèves en évitant cette redondance grâce à des énoncés qui ne comportent que le texte ou que la figure, on pourra les y habituer peu à peu, même tout au long du collège, puisqu’ils en rencontreront dans des manuels, voire des sujets d’examens.
Ensuite, la figure donnée dans cet énoncé semble être tracée avec des instruments. On peut considérer qu’il est prématuré en 6e de donner des figures « propres » en les considérant comme de simples schémas. Il est possible de la remplacer par une figure faite « à main levée » (non tracée à la règle, avec des traits raisonnablement tremblants) qui aidera l’élève à se placer en géométrie du raisonnement, sans avoir à lui dire qu’il ne doit pas mesurer avec son rapporteur.
Par ailleurs, le manuel proposait cet exercice comme exemple d’exercice résolu. Cette méthode est reconnue comme pouvant aider les élèves à comprendre les attendus, notamment en termes de rédaction de la solution. Cependant, dans les extraits de manuels suivants, on peut considérer que les communications écrites du raisonnement et du calcul sont trop exigeantes dans la phase d’apprentissage des élèves :

(Transmath 6e 2025, page 187)

(Mission Indigo 6e 2025, page 215)
Le professeur distinguera la phase d’apprentissage du raisonnement et du calcul à étapes, de la phase d’apprentissage de leur communication. Pour baisser la charge cognitive des élèves, il pourra accepter dans un premier temps des réponses très courtes où l’élève montre qu’il a compris ce qu’il faisait comme :
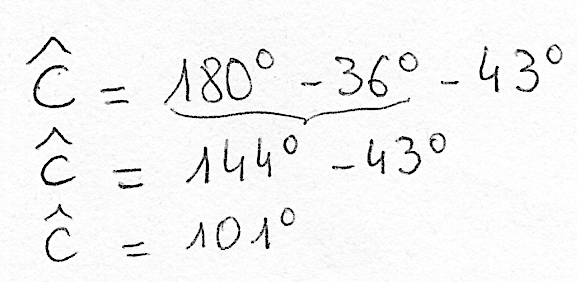
On peut proposer ce type d’exercice en exercice d’automatisme lié au calcul mental, sur une ardoise par exemple.
Ainsi, beaucoup d’élèves commencent le calcul sans le justifier par la récitation de la propriété, tout en annonçant qu’ils cherchent l’angle par une soustraction. Leur faire écrire la somme des angles au départ, pour exiger le remplacement par les mesures connues et mener une résolution d’équation est tout à fait prématuré. Cela n’est pas exigible au collège, alors que la justification avec la propriété va l’être peu à peu, mais pas pour tous les élèves en autonomie. Même à l’écrit, on pourra demander à ceux qui sont en difficulté de réciter la propriété avant de donner l’exercice.
Le professeur, quant à lui, pourra continuer à montrer comment rédiger de façon de plus en plus académique en explicitant qu’il ne l’attend pas en évaluation.


