Présentation

En classe de terminale générale, l’enseignement optionnel de mathématiques complémentaires est destiné prioritairement aux élèves qui :

• ont suivi l’enseignement de spécialité de mathématiques en classe de première et ne souhaitent pas poursuivre cet enseignement en classe terminale,
• ont besoin de compléter leurs connaissances et compétences mathématiques par un enseignement adapté à leur poursuite d’études dans l’enseignement supérieur (par exemple en médecine, SVT, économie, sciences sociales, psychologie, STAPS, en licence, en IUT ou en BTS).

Le programme de mathématiques complémentaires s’appuie sur le programme de spécialité de mathématiques de la classe de première qu’il réinvestit et enrichit de nouvelles connaissances et compétences mathématiques, elles-mêmes reliées à des thèmes d’étude où les notions sont mises en situation dans divers champs disciplinaires.

Pour le baccalauréat, l’option mathématiques complémentaires ne donne pas lieu à une épreuve terminale ni à une E3C, elle est prise en compte uniquement via les notes des bulletins de terminale, qui interviennent avec celles de la classe de 1^re pour 10 % de la note finale. Si elle pèse moins de 1 % de la note du bac, cette option relève d’un réel enjeu de complément de formation en mathématiques pour les élèves ayant un projet d’études en relation avec les mathématiques.

Des thèmes d’étude et des notions

Le programme est écrit selon deux entrées : 9 thèmes d’étude, où les concepts mathématiques sont mis en situation dans divers champs disciplinaires, et un ensemble de contenus et capacités attendues. L’objectif est de traiter l’ensemble des contenus et capacités attendues au travers des thèmes d’étude.

Le professeur choisit sa façon de travailler le thème d’étude en fonction des goûts des élèves, de leur choix de spécialités et de leur projet d’études supérieures. Les compétences de modélisation et de communication sont particulièrement mises en valeur, mais toutes les compétences mathématiques sont mobilisées, notamment le raisonnement et la capacité à construire une démonstration.

Les thèmes d’étude constituent une approche nouvelle pour l’enseignant de mathématiques, plus habitué à une progression par notions.

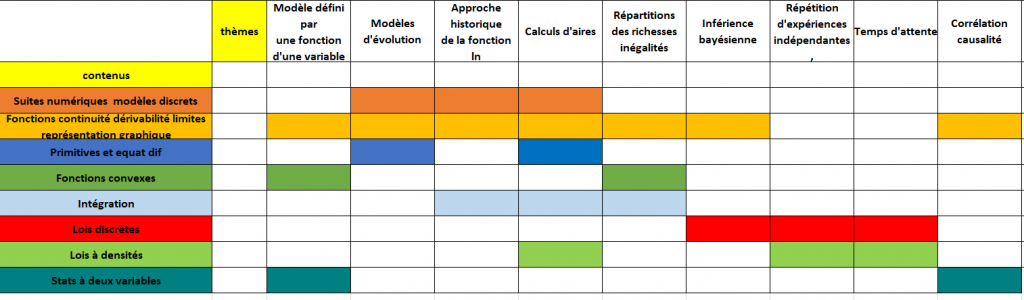
Un exemple de progression par thèmes

L’enseignant peut construire une progression par notions ou par thèmes. L’approche par thèmes semble cependant se situer davantage dans l’esprit des programmes, elle permet à la fois une progressivité et une consolidation des notions du programme, ainsi que des approfondissements et colorations disciplinaires selon les intérêts et les projets d’orientation des élèves.

Les formateurs de l’académie de Bordeaux vous proposent une progression décomposée en 11 séquences thématiques. Chaque notion mathématique du programme apparaît ainsi dans plusieurs séquences.

1. 1. Modèles d’évolution 1
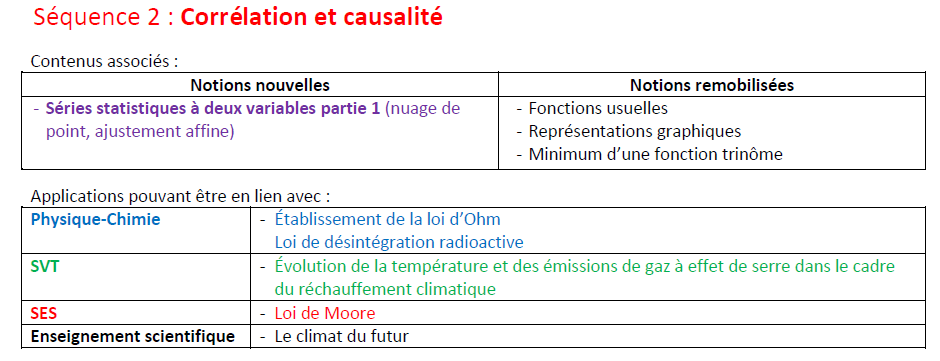
   2. Corrélation et causalité
   3. Modèles définis par une fonction d’une variable 1
   4. Inférence bayésienne
   5. Modèles d’évolution 2
   6. Calculs d’aires
   7. Répétition d’expériences indépendantes, échantillonnage
   8. Approche historique de la fonction logarithme
   9. Modèles définis par une fonction d’une variable 2
   10. Répartition des richesses, inégalités
   11. Temps d’attente

Chaque séquence sera naturellement constituée d’activités variées : de problèmes en lien avec le thème, de temps de cours sur des notions et d’exercices d’entraînement. Pour chaque séquence, la progression précise :

• Les contenus associés
  • Les notions nouvelles du programme de l’option Mathématiques Complémentaires
  • Les notions antérieures (étudiées lors des années précédentes)
• Des applications pouvant être en lien avec le thème de la séquence (problèmes possibles du programme, liens avec l’autre spécialité, enseignement scientifique, culture mathématique)

Consultez la proposition de progression par thèmes pour l’Option Maths Complémentaires

Remarque : cette progression n’est qu’une proposition présentée à l’occasion des premières formations de mars 2020 sur la réforme de lycée dans l’académie de Bordeaux. Elle pourra évoluer par la suite.

Autres ressources

• Ressources de formation de l’académie d’Aix-Marseilles