Boîte

Objectifs

Résoudre un problème d’optimisation :

•  En 3^ème ou en seconde : Calcul littéral – Utilisation de la représentation graphique d’une fonction pour conjecturer un maximum. Éventuellement un prolongement possible en utilisant un tableur pour encadrer la solution du problème.
•  En 1^ère : Étude d’une fonction polynôme de degré 3.

Prérequis

•  Patron et volume du parallélépipède rectangle.
•  Notion de fonction.

Énoncé

On dispose d’une plaque rectangulaire cartonnée de dimensions 120 cm sur 80 cm.   Pour des raisons économiques, on veut découper dans ce carton le patron d’une boîte parallélépipédique ayant un volume maximal.

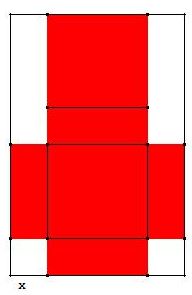Déroulement de la séquence

•  Faire construire aux élèves le patron d’un parallélépipède rectangle dans un cadre de dimensions 12 cm sur 8 cm. Indiquer les dimensions choisies puis calculer le volume du patron dessiné.

•  En classe: utilisation de GeoplanGeospace pour visualiser le patron, le pavé droit et son volume à l’aide de figures communicantes ouvertes en mosaïque verticale (on pilote la variable x dans le fichier « boite_patron.g2w », on peut ouvrir le patron à l’aide des flèches du clavier dans le fichier « boite.g3w » et le placer en vue de face à l’aide la touche P).
  On peut ensuite ouvrir le fichier « boite_courbe.g2w » et le placer lui aussi en mosaïque verticale afin de visualiser les variations du volume de la boîte

Documents

• Fichier patron Boite(geoplan)
• Fichier Boite (geospace)
• Fichier courbe Boite (geoplan)