Pour répondre à une demande faite par les participants au stage PAF sur la pratique du problème ouvert en mathématiques, nous avons créé cet espace de mutualisation de questions ouvertes testées dans nos classes de collège et lycée.
Les énoncés et activités proposés ne doivent pas être considérés comme des modèles mais comme une occasion de travailler ensemble.
Si vous avez expérimenté d’autres sujets, vous pouvez les transmettre avec quelques commentaires sur la mise en œuvre et les réactions des élèves à referentmath02@ac-bordeaux.fr
Nous avons classé ces questions ouvertes par thèmes, en indiquant les niveaux auxquels il nous semble possible de les proposer.
Du numérique au littéral
Points et segments (6e > TS)
Source
« Les narrations de recherche de l’école primaire au lycée » – IREM Montpellier
Problème
Étant donné plusieurs points sur une feuille, combien peut-on tracer de segments joignant deux quelconques de ces points ?
Fichiers disponibles
Commentaires
Proposé en narration de recherche, en 3e et en 5e (sans la ligne « n points »).
Tous les élèves ont proposé quelque chose, car ils ont pu au moins réaliser des figures pour compléter les premières lignes du tableau. Beaucoup ont très vite trouvé la relation permettant de passer d’une ligne à l’autre, mais ont remarqué qu’elle permet difficilement de trouver le nombre de segments pour n points.
Parmi ceux qui ont cherché une relation générale entre le nombre de points et le nombre de segments, beaucoup l’ont fait par observation du tableau et par essais de différentes formules. Quelques-uns sont arrivés à justifier la formule en raisonnant sur les figures (nombre des segments tracés à partir d’un point donné)
Château de cartes (4e > 1S)
Source
Les narrations de recherche de l’école primaire au lycée – IREM Montpellier
Problème
Un château de cartes est un empilage organisé de la façon suivante :
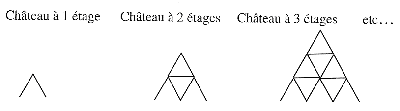
Combien faut-il de cartes pour construire 5 étages, 12 étages, 100 étages et, de manière générale, n étages ?
Fichiers disponibles
Commentaires
Proposé en narration de recherche en classe de 3e
Les élèves ont mis en place des procédures personnelles pour compter les cartes dans des cas simples ; ils ont ensuite conjecturé une formule qu’ils ont vérifiée à l’aide de leurs premiers résultats.
Pour faire la synthèse des travaux des élèves, l’enseignant a répertorié parmi les différentes productions les méthodes pertinentes.
Disposant d’un tableau numérique, il a préparé un paperboard de plusieurs feuilles qui permettront aux élèves de présenter leur démarche devant la classe ; le choix a été fait d’illustrer les différentes procédures sur le même nombre d’étages, ce qui est ici plus clair que de travailler sur des scans de copies.
Le TNI permet de garder les traces de toutes ces procédures afin d’en faire un bilan et de montrer qu’elles aboutissent toutes au même résultat.
TNI = « Tableau Numérique Interactif
Configurations du plan
Agrandissement (4e > TS)
Source
Les narrations de recherche de l’école primaire au lycée – IREM Montpellier
Problème
Construire deux carrés de telle sorte que l’aire du deuxième soit le double de l’aire de l’autre.
Commentaires
Activité proposée en narration de recherche.
La plupart des élèves ont cherché une solution calculatoire : doubler la longueur du côté, multiplier par 1,5, utiliser une valeur approchée de la racine carrée. D’autres ont utilisé une solution géométrique, en découpant le carré de départ en carrés ou en triangles et en essayant de les doubler.
Aire maximale (1e > TS)
Problème
ABCD est un carré de 4 cm de côté. E est le milieu de [AD].
On considère un point M du segment [AB].
La perpendiculaire en M à la droite (EM) coupe le segment [BC] en N.
Déterminer pour quelle(s) position(s) de M sur [AB] l’aire du triangle EMN est maximale.
Fichier disponible
Commentaires
Exercice donné en début d’année de terminale S, d’abord à chercher seuls (beaucoup de difficultés !), puis cherché par groupes de deux en demi-classe.
Bouge ou bouge pas ? (4e > 2e)
Source
Magnard 4e
Problème
On considère un segment [AB] et C un point quelconque n’appartenant pas à la droite (AB).
C’ est le point de [CA) tel que C’A = 6 CA.
I est le milieu de [AC’] et K est le milieu de [BC’].
(CK) coupe (AB) en M.
Le point M change-t-il de position si l’on déplace C ?
Fichier disponible
Commentaires
Exercice proposé en 3e, d’abord à chercher seuls.
De nombreux élèves ont tout de suite conclu que le point M change évidemment de position, sans chercher à tester leur conjecture ; d’autres ont réalisé plusieurs figures pour voir ce qui se passait.
La synthèse avec utilisation de Geoplan a permis de valider on non les conjectures, puis de mettre en place la démonstration.
Carré-Triangle (2e > TS)
Problème
On considère un carré direct ABCD du plan orienté.
À tout point M du segment [AB] privé de A, on associe le point P tel que le triangle APM soit direct, rectangle et isocèle en A.
Conjecturer le résultat relatif à la position des droites (BP) et (DM), puis le démontrer.
Fichier disponible
Commentaires
Donnée en terminale, cette question ouverte a été traitée en classe : recherche individuelle pendant 20 minutes, à rédiger sur feuille.
Trois méthodes ont été utilisées : rotation de centre A et d’angle pi/2, calcul vectoriel et produit scalaire, choix d’un repère orthonormal.
L’orthocentre ou des triangles semblables ou isométriques étaient d’autres pistes possibles.
Lieux géométriques
Intersection de deux cercles (3e > TS)
Problème
Soit une droite (d) et deux points A et B en dehors de cette droite. À tout point M de (d), on associe le deuxième point M’ d’intersection des cercles de centres respectifs A et B et passant par M.
Quel est le lieu de M’ quand M décrit (d) ?
Fichier disponible
Points mobiles (1e > TS)
Problème
On considère un segment [AB] et M un point mobile sur ce segment.
Dans l’un des demi-plans de frontière (AB), on construit K et L tels que AKM et MLB soient rectangles isocèles respectivement en K et L.
I est le milieu de [KL]
Comment I se déplace-t-il lorsque M se déplace sur [AB] ?
Fichier disponible
Un lieu de points (2e > 1eS)
Problème
On considère trois points O, A et B.
Un point M se déplace sur le cercle de diamètre [AB], et un point N se déplace simultanément de façon que le triangle MON reste rectangle et isocèle en O, les points O, M et N se lisant dans le sens des aiguilles d’une montre.
Sur quelle ligne le point N se déplace-t-il ?
Fichier disponible
Voir dans l’espace
Cube et distance (3e > 1S)
Source
Les narrations de recherche de l’école primaire au lycée – IREM Montpellier
Problème
ABCDEFGH est un cube d’arête 10 cm.
Combien existe-t-il de points sur les arêtes du cube à 15 cm de A ?
Fichier disponible
Commentaires
Proposé en narration de recherche en 3e.
Certains élèves ont essayé d’utiliser le compas : soit sur le cube en perspective (en ayant plus ou moins conscience de la perspective), soit sur le patron.
Certains ont même envisagé plusieurs cas selon la position du point A…
D’autres ont eu recours au théorème de Pythagore, mais se sont souvent arrêtés au calcul de la diagonale d’une face et ont conclu que ce n’était pas possible.
Parallélisme dans l’espace (2e > TS)
Problème
K et L sont deux points sur les arêtes [EH] et [EF] du parallélépipède rectangle ABCDEFGH.
Les droites (AK) et (DH) se coupent en M.
Les droites (AL) et (BF) se coupent en N.
Comment doivent être placés les points K et L pour que les droites (KL) et (MN) soient parallèles ?
Fichier disponible
Grand angle (TS)
Source
Problèmes à chercher – IREM Grenoble
Problème
On considère un cube ABCDEF. Pour fixer les idées, faire un dessin en perspective cavalière avec ABCD face de dessous, ABFE face avant et EFGH face de dessus.
Pour quelle position du point M sur la diagonale (HB), l’angle AMC est-il le plus grand ?
Fichier disponible
Commentaires
Travail de groupe en TD.
Les élèves disposent du logiciel Geospace (une rapide présentation du logiciel a été faite à cette occasion) et de deux fiches (travail à effectuer et fiche de synthèse).
La rédaction d’une solution a fait l’objet d’un travail à la maison.
Plus court chemin
Triangles rectangles (4e > TS)
Problème
ABC est un triangle rectangle en A.
M est un point de l’hypoténuse [BC].
On trace par M les perpendiculaires aux côtés [AB] et [AC] qui coupent ces côtés respectivement aux points P et Q.
Où placer le point M pour que la distance PQ soit minimale ?
Fichier disponible
Fichiers triangles rectangles Activité, Géoplan, GeoGebra
Commentaires
Proposé en 4e, d’abord à chercher seuls.
Presque tous les élèves ont eu l’idée de réaliser plusieurs figures, avec le même triangle de départ, mais en modifiant la position de M. Des conjectures très diverses ont été proposées car beaucoup ont cherché à caractériser la position de M par sa position sur le segment [BC] (M doit être au milieu, au quart, au tiers… du segment [BC], sur la bissectrice de l’angle BAC, sur la hauteur issue de A…).
La synthèse avec Geoplan a permis de valider ou non les conjectures, puis de mettre en place la démonstration, en faisant apparaître la deuxième diagonale du rectangle APMQ.
Proposé en temps libre en terminale avec la possibilité de travailler par deux ou trois et de ne rendre qu’une copie pour le groupe.
Sur plus de la moitié des copies, une solution est proposée avec de la géométrie analytique. Dans le repère
![]()
L’équation de la droite (BC) permet d’écrire les coordonnées de M puis celles de P et Q et enfin . Il reste à étudier le minimum d’une fonction trinôme…
La synthèse des démarches était instructive…
Bibi la souris (4e > TS)
Source
Dimathème 4e
Problème
SABCD est une pyramide à base carrée de 6 cm de côté et dont les faces latérales sont des triangles équilatéraux.
Bibi la souris doit se rendre par le chemin le plus court du point A au point J, milieu de [SC], en se déplaçant à la surface de la pyramide.
Trouver la position de T sur l’arête [SB] qui donne le plus court chemin, ainsi que la longueur de ce trajet.
Fichier disponible
Commentaires
Activité proposée en temps libre en terminale.
Certains élèves ont cherché à exprimer la distance AJ en fonction de x = BT, ce qui conduit à l’étude des variations d’une fonction irrationnelle…
Arithmétique
Puissances (4e > TS)
Source
Les narrations de recherche de l’école primaire au lycée – IREM Montpellier
Problème
Si je calcule 131, le chiffre des unités est 3.
Si je calcule 132, le chiffre des unités est 9.
Quel est le chiffre des unités de 133, 134, 135 ?
Quel est le chiffre des unités de 132006 ?
Commentaires
Activité proposée en narration de recherche en 4e.
Beaucoup d’élèves ont pensé qu’il suffisait de trouver le chiffre des unités de 36, ce qui ici donne la solution, mais qui ne peut bien sûr pas se généraliser ; cela a pu être abordé lors de la correction à l’aide de contre-exemples.
Plusieurs élèves ont remarqué la périodicité des chiffres, et ont trouvé la solution à l’aide d’une division euclidienne.
Décomposition de 1 (TS)
Problème
Soit un entier naturel n >= 3
Peut-on écrire 1 sous la forme de la somme des inverses de n entiers naturels distincts deux à deux ?
Autrement dit, existe-t-il n entiers différents deux à deux, tels que :
![]()
Commentaires
Activité proposée en devoir maison.
Tous les élèves ont expérimenté, mais la plupart ont été démunis pour rédiger une solution.
Certains ont pensé à mettre en œuvre un raisonnement par récurrence.
Suites
Suite avec racine (TS)
Problème

Commentaires
Un des premiers exemples de l’année, proposé en classe entière, après acquisition du raisonnement par récurrence (on peut aussi utiliser un raisonnement « de proche en proche » comme en 1re S).
Certains expérimentent spontanément numériquement ; d’autres se lancent dans le tracé de la courbe représentant la fonction ![]() .
.
n3n8 (1e > TS)
Problème
On pose :
![]()
La suite (un) est-elle convergente ? Si oui, déterminer sa limite.
Commentaires
Activité proposée en terminale après avoir traité le raisonnement par récurrence et les suites monotones bornées, mais longtemps après…
Recherche effectuée en demi-groupe
Dès le début les élèves ont eu l’intuition que cette suite convergeait vers 4/3.
Fonctions
Racine dans R d’un polynôme de degré trois (TS)
Problème
Tout polynôme de degré trois admet-il une racine dans R ?
Une tentative de généralisation ?
Commentaires
Activité proposée en temps libre.
Inflexion impaire (TS)
Problème
1. Tracer la courbe représentative de la fonction définie par f(x) = x3 dans un repère du plan d’origine O et étudier la position de cette courbe par rapport à sa tangente en O.
2. On considére une fonction f impaire et dérivable sur R. Sa courbe représentative traverse-t-elle sa tangente au point d’abscisse zéro ?
Commentaires
Activité proposée en temps libre.
Position relative (TS)
Problème
Tracer les courbes représentatives respectives des fonctions
![]()
en justifiant ces tracés.
Quelle conjecture peut-on faire quant aux positions respectives de ces deux courbes ?
Démontrer la propriété observée.
Commentaires
Activité proposée en demi-groupe, après l’étude de la croissance comparée de la fonction exponentielle et de la fonction identique.
Pour la première question, les élèves doivent déterminer seuls ce qui est nécessaire pour tracer avec certitude les courbes.
Intégrales
Lien entre intégrales (TS)
Problème
Soit a un réel de ] 0 ; 1 [.
Peut-on établir une relation entre
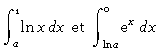
Commentaires
Proposé en demi-groupe après la première partie du cours sur l’intégrale mais avant d’avoir traité l’intégration par parties, cet exercice peut aussi être proposé en temps libre. Avec un très bon groupe, il peut même être proposé en devoir surveillé.
Interprétation en termes d’aire. Les élèves savent que les courbes des fonctions ln et exp sont symétriques par rapport à la première bissectrice du repère.


