TraAM 2023-2024 – “Pensées-réflexes” bien automatisées ou erronées ?

Sommaire des traAm 2023/2024 “esprit critique”.

Caractéristiques

• Thématique

Face à une question d’un Vrai/Faux ou d’un QCM, comment décider vite et bien ? Qu’est-ce qui est à l’œuvre dans nos pensées, entre le réflexe qui nous empêche de douter et la “peur” des pièges ou des trompe-l’œil qui nous fait hésiter ?

• Problématique

Comment raisonner vite et bien ? Dans Apprendre à résister (Flammarion, 2022), le chercheur Olivier Houdé part de la modélisation du fonctionnement du cerveau par un double système : le système 1 basé sur des automatismes et le système 2 représentant des circuits plus longs et activant des algorithmes et des logiques exactes. Il ajoute à ce modèle un système 3 : celui de l’inhibition, fonction exécutive et protectrice très importante de notre cerveau. Apprendre à évaluer si la situation rencontrée peut être biaisée est essentiel et nécessite un ralentissement de la pensée automatique, un blocage du système 1 pour une activation du système 2. Il faut aussi ne pas douter lorsque la situation ne présente pas de piège particulier, et il apparaît donc utile de détecter, nommer et expliciter les biais qui ont agi dans les prises de décision.

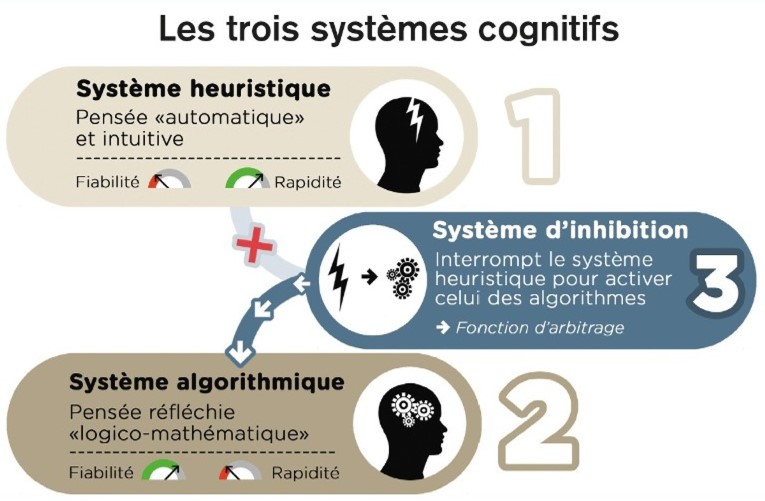
• Contenus et objectifs disciplinaires

Logique, calcul mental et algébrique, suites

Scénario

1^ère séance (10 min) : 17 élèves de Terminale Spécialité Mathématiques, répondent, avec leur téléphone portable, à un questionnaire numérique créé avec l’application KAHOOT par le professeur.

Il est vidéo-projeté en classe, présenté comme un jeu. Bien qu’un classement, non anonyme, soit proposé, les élèves sont informés que les résultats ne seront pas comptabilisés dans l’évaluation du trimestre.

Ce questionnaire est composé de 5 questions ; il est minuté (30 secondes par question) et les élèves sont prévenus du fait qu’il s’agit de trouver la seule bonne réponse à chaque question, et que le temps de réponse est pris en compte dans le nombre de points attribué à chaque bonne réponse.

Les questions défilent toutes les 30 secondes :

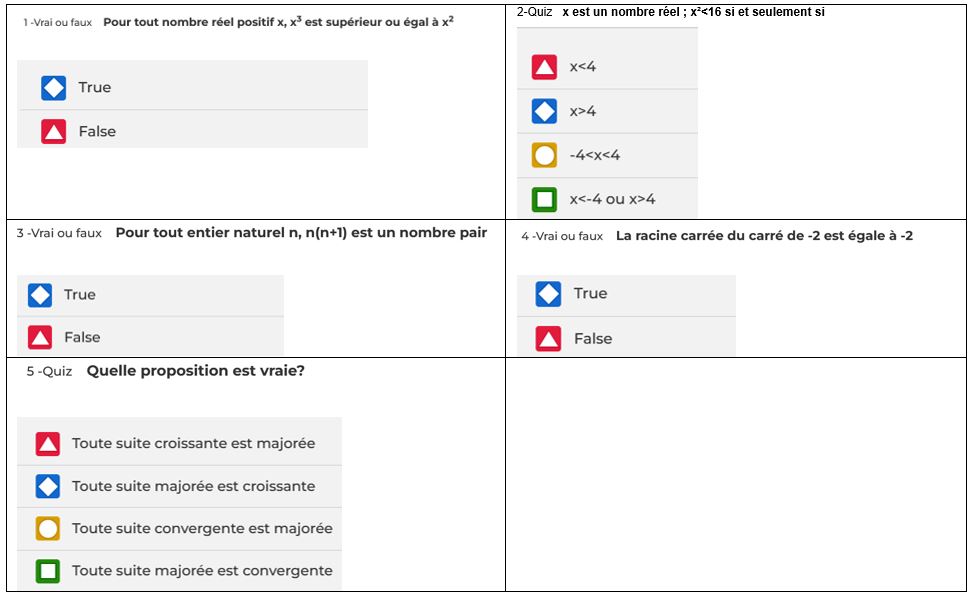
2^nde séance (1 heure) : quelques jours après

• 5 groupes, constitués par le professeur, mènent une correction concertée des 5 questions. Le groupe écrit et justifie la bonne réponse concertée de chaque question sur un polycopié distribué par le professeur.

• Ensuite, chaque groupe a en charge l’analyse des résultats d’une des 5 questions (Groupe 1/Question 1, Groupe 2/Question 2, etc…) : chaque élève dispose du taux de réussite de la classe sur chaque question, de son propre résultat au questionnaire, du temps passé sur chaque question, du nombre de points qui en découle pour ses bonnes réponses, et enfin de classement. Ci-dessous : consignes passées, extrait du polycopié à remplir, exemple de résultat individuel d’un élève.

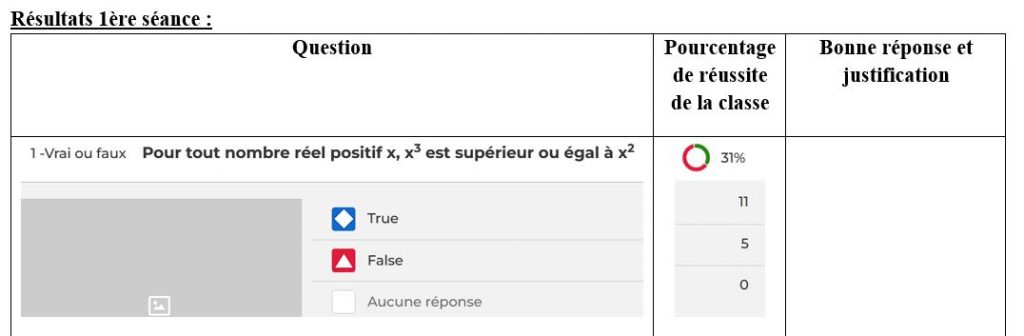
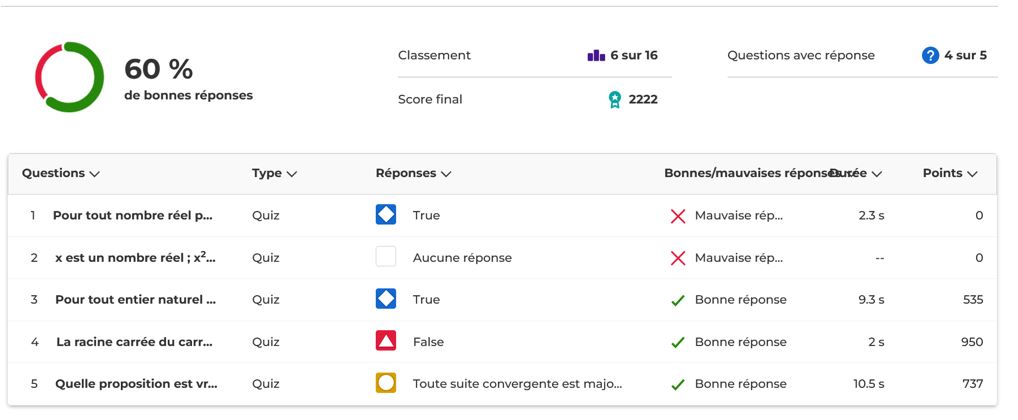
Les compétences

Compétences du CRCN-édu  mobilisées par l’enseignant

Domaine 1 – DÉVELOPPEMENT PROFESSIONNEL

• 1.5 Adopter une posture ouverte, critique et réflexive

Domaine 3 – ENSEIGNEMENT-APPRENTISSAGE

• 3.1 Concevoir

• 3.3 Évaluer au service des apprentissages

Déroulement des séances

Déroulé de la 1ère séance

Le professeur a expliqué les consignes et le format du questionnaire puis lancé le travail numérique avec l’application KAHOOT, puis le podium est apparu avec le nombre de points obtenu par les 3 premiers, selon leur taux de réussite et leur temps de réponse . (10 min)

Déroulé de la 2nde séance

Le professeur a évoqué de nouveau le questionnaire et présenté la seconde séance. (2 min)

Il a ventilé les élèves en 5 groupes et distribué la fiche élève de la 2^nde séance, puis reformulé les consignes. (5 min)

Chaque groupe a corrigé les 5 questions, mais n’a analysé que celle dont il avait la charge, puis a écrit un bilan. (30 min)

Restitution orale de chaque groupe. (10 min)

Le professeur a fait un bilan et fait le lien entre l’analyse des élèves des premiers biais cognitifs repérés. (5 min)

Constats et commentaires sur le travail des élèves et de chaque groupe durant les 2 séances

Lors de la 1^ère séance, 17 élèves étaient présents, mais une élève, qui n’avait pas de téléphone opérationnel, a constitué un binôme avec une camarade. Certains élèves ont trouvé le temps trop court pour certaines questions et l’ont exprimé.

Lors de la 2^nde séance, les groupes ont dû se mettre d’accord, puis mener un raisonnement, dans les différents domaines mathématiques, pour démontrer. Au sein de chaque groupe les élèves ont dû partager leurs idées afin d’élaborer une correction commune. Les compétences « raisonner » et « communiquer » ont été mobilisées.

Les élèves ont bien joué le jeu. Certains ont interrogé le professeur sur l’intérêt de décortiquer les raisons des réussites ou des erreurs. Les élèves se seraient contentés de produire une réponse argumentée aux différentes questions.

Même si le questionnaire ressemblait au travail ritualisé des automatismes sous une forme différente, le professeur a donc eu du mal à légitimer ce travail d’identification de biais relatifs au fonctionnement du cerveau au regard des contenus habituels du cours de mathématiques. La présentation de cette activité a donc pu introduire un biais de cadrage. La recherche de ces biais paraissait soit incongrue, soit inutile car ne comptant pas dans la moyenne, soit stressante du fait de la compétition induite. Le choix a donc été fait de ne pas présenter les 3 systèmes de Houdé ni un exposé sur les biais cognitifs lors de ces séances.

Productions des groupes d’élèves et analyse des biais à l’œuvre lors de l’exercice KAHOOT

Groupe 1/Question 1

Analyse Q1 : dans l’analyse écrite, on trouve : ” On pense  directement aux nombres entiers”. On peut émettre l’hypothèse qu’apparait ici un biais de confirmation : on a inconsciemment tendance à chercher des informations qui renforcent nos croyances et à rejeter ou relativiser les informations qui les réfutent. Ici, comme la propriété est vraie pour les nombres entiers, on croit qu’elle est vraie pou tout réel.

Groupe 2/Question 2

Analyse Q2 : dans l’analyse écrite, on trouve : ” Pas le temps” et “On ne sait pas la signification des > et <“. Il est probable que cette question soit difficilement lisible telle qu’elle a été posée. Avec des intervalles, cela aurait peut-être aidé. La question du temps est prégnante : le professeur que la bonne réponse était évidente, mais la question semble nécessiter, même en terminale, plus de temps. Ce n’est pas une bonne question pour tester si des réflexes viennent vite et bien ! Le stress lié au temps peut déclencher le système d’inhibition pour de mauvaises raisons.

Groupe 3/Question 3

Analyse Q3 : dans l’analyse écrite, on trouve : ” Temps trop court” et “Hasard”. Il est probable que le stress dû à la limitation en temps entre en ligne de compte dans l’expérimentation : la disponibilité d’esprit a manqué ou la menace de la double évaluation (temps+bonne réponse) a pris le dessus. Le professeur a pensé, là encore, qu’un bon réflexe serait d’avoir assez vite la bonne réponse. La question du hasard apparaît : pour “gagner”. Sur une question qui n’est pas évidente, l’élève ne fait pas la différence entre : « répondre rapidement au hasard », « réfléchir et répondre faux » ou « ne pas répondre du tout ».

Groupe 4/Question 4

Analyse Q4 : un bon taux de réussite. Néanmoins, à l’oral, un élève a dit : « on a compris le carré, puis la racine carrée, puis que l’un  compense l’autre, donc normalement on retombe sur le nombre” . Dans l’analyse écrite, on trouve : ” Ceux qui ont faux ont surement du se précipiter et être perturbés par la racine carrée avant le carré”. L’hypothèse du biais de rejet et enfermement dans la croyance initiale en raison de son coût est plausible : plus on a utilisé d’énergie, de temps, … à adopter une croyance, plus on aura du mal à l’abandonner quand on voudra nous convaincre qu’elle est erronée.

Groupe 5/Question 5

Analyse Q5 : dans les résultats de la classe, on voit qu’il y a surtout eu hésitation entre les 2 dernières réponses possibles. Dans l’analyse écrite, on trouve : ” Confusion du théorème de convergence monotone avec le cas général” et “Formulations semblables peut-être difficiles à comprendre/distinguer rapidement”. De plus, à l’oral, un élève a dit : « quand il y a croissante ou majorée dans la phrase, on croit que c’est vrai qu’elle est convergente” . Le temps semble encore mettre une pression qui empêche d’entrer sereinement dans un raisonnement. Un biais sélectif de données peut être présent dans cette question. Les choix faits par le professeur est souvent de présenter des suites majorées ET croissantes, reléguant ainsi les suites majorées, non croissantes, à des exemples peu rencontrés. Le cerveau des élèves n’étant pas suffisamment mis en contact avec des suites majorées et non convergentes, a tendance à négliger ce cas, au profit des cas fréquemment rencontrés.

Bilan final du dispositif et perspectives

Le côté ludique du support utilisé (compétition non notée, les exæquo sont départagés par le temps) aura quand même fait son effet et l’engagement des élèves dans cet exercice est naturel. Même s’il y a une part de hasard dans les décisions qu’on doit prendre vite et bien, nous avons constaté que notre réaction (automatique ou réfléchie) face à des questions dépendait de différents paramètres :

• le hasard

• le stress lié au temps de réponse

• le niveau d’assimilation des notions

• le formalisme et la formulation de la question

L’expérimentation de ce dispositif met donc en jeu à la fois les savoirs mais aussi les compétences psycho-sociales (émotions, gestion du stress, pensée critique). Elle n’a pas, à ce stade, réussi à définir plus précisément quand et comment inhiber le système 1 (intuitif) pour laisser place au système 2 (réfléchi). Comment déclencher le système 3 ? Pour y parvenir davantage, et notamment faire émerger et expérimenter des biais cognitifs dans de meilleures conditions, voici quelques conclusions qui s’imposent, faisant également office de perspectives de travail.

On pourrait essayer de séparer la question du temps limité de celle de la problématique de l’inhibition (ou non) du système intuitif : on pourrait par exemple imaginer un questionnaire identique posé sans limite de temps, pour éliminer l’effet de stress temporel. On pourrait aussi comparer le même questionnaire avec ou sans prise en compte du temps de réponse dans la performance.

On pourrait essayer de prendre en compte le temps de réponse uniquement lorsque les questions sont simples, c’est à dire vraiment quand il faut actionner rapidement l’automatisme ou rapidement se méfier. Or dans notre expérimentation, le temps donné pour les questions 2 et 3 n’était peut-être pas suffisant pour décider ou la question trop abstraite, alors que justement le professeur les avait conçues comme celles où la réponse devait être « évidente » assez vite. 

On pourrait essayer d’ouvrir un champ de questions plus large et plus varié, moins mathématiquement techniques, ou moins mathématiques et à d’autres niveaux de classe (2nde, 1ère…)

On pourrait essayer d’analyser les biais qui sont à l’œuvre dans les analyses des groupes, ou de faire répondre au questionnaire en en groupes, de façon à faire collaborer les élèves et sensibiliser à d’autres biais importants liés à la vie en société, qui modifient la décision ou altèrent l’esprit critique : biais d’autorité, effet de halo, effet de groupe, influence de nos émotions…

Ce dispositif peut être le moyen de s’entraîner à une mise en situation répétée et fréquente de décisions à prendre, où non seulement on corrige le questionnaire à chaque fois mais on analyse en plus les taux de réussite et les raisons qui ont conduit aux échecs. Les biais pourront être alors peu à peu conscientisés et régulièrement répertoriés avec le professeur. Ce dispositif peut être une entrée ludique et non descendante dans un enseignement intégrant peu à peu certains aspects de l’esprit critique et certaines compétences psycho-sociales.

Outils et ressources

Fiche élève de la 2nde séance

Enseigner les mathématiques avec les sciences cognitives : la théorie des trois systèmes d’Olivier Houdé

https://academiesciencesmoralesetpolitiques.fr/membres-titulaires/section-i-philosophie-2/olivier-houde/

Tuto de l’académie de Rennes pour l’application KAHOOT : https://pedagogie.ac-rennes.fr/sites/pedagogie.ac-rennes.fr/IMG/pdf/kahoot.pdf