Objectifs
Résolution d’un problème par une approche graphique et fonctionnelle.
Prérequis
- Notion de fonction
- Calculs de volumes
- Réduction
- Équation produit
Déroulement de la séquence
En classe entière à l’aide d’un vidéoprojecteur.
- Présentation du problème à l’aide de la figure Geospace (pyramide_pave.g3w) qui permet de faire varier h.
- Ouvrir la figure Geoplan (pyramide_pave.g2w) et la mettre en mosaïque verticale afin d’observer
les variations des volumes en fonction de h. - L’outil Geoplan-Geospace ne permet pas (même en diminuant le pas de h) de conjecturer la valeur exacte de h ; la résolution mathématique du problème est indispensable.
- L’approche fonctionnelle amène à une résolution par mise en équation ; après factorisation il faut résoudre une équation produit.
- On peut mettre en évidence une autre méthode utilisant la proportionnalité du volume d’une pyramide à celui d’un pavé de même base. On peut ensuite rechercher le coefficient de réduction entre les deux pyramides (récipient et eau).
Des commandes permettent de faire apparaître :
– le pavé lié à la pyramide d’eau : touche 1
– le rapport des aires des bases des deux pyramides : touche 2
– le rapport des hauteurs des deux pyramides : touche 3.
Énoncé :
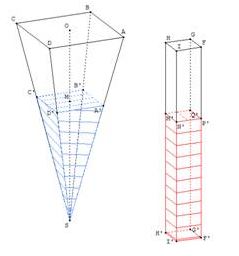
| On dispose de deux récipients :
– Le premier a la forme d’une pyramide régulière (posée sur son sommet) de hauteur 15 cm et dont la base est un carré de côté 6 cm. – Le deuxième a la forme d’un parallélépipède rectangle de hauteur 15 cm et dont la base est un carré de côté de 2 cm. On remplit les récipients avec une même hauteur h d’eau. Y a-t-il une hauteur h pour laquelle les deux volumes d’eau sont égaux ? |
 |


