Apparences trompeuses ? Automatismes et représentations de données, esprit critique

Sommaire des TraAM 2023/2024 “esprit critique”.

Caractéristiques

• Thématique

Les objectifs sont d’apprendre à se questionner dans la vie courante et d’apprendre à optimiser nos automatismes afin d’acquérir de bons réflexes face à des situations rencontrées dans la vie courante : on va chercher à améliorer l’inhibition, c’est-à-dire savoir à éduquer son cerveau pour bloquer sa première pensée lorsqu’elle risque d’être trop simpliste voire erronée parce qu’elle a été trop rapide, à améliorer sa compréhension, et donc, in fine, son esprit critique.

Des situations réelles sont analysées en petites séries sous la forme de questions-flash, lors de séances différentes, filées sur l’année scolaire. Les photographies authentiques issues de différents médias amènent à s’interroger sur les erreurs mathématiques que l’on peut rencontrer (diagrammes, prix et réductions, modèle de la proportionnalité).

• Problématique

Les mathématiques sont utilisées pour annoncer des promotions, préciser des dosages, représenter visuellement des données, … Quelles questions peut-on se poser ? De quoi peuvent relever les erreurs mathématiques ? Comment peut-on les interpréter et quelles conséquences ont-elles ? Dans quelles situations faut-il être particulièrement prudent à la lecture de ces informations ? Qu’est-ce qui peut nous tromper (cas des erreurs de bonne foi, cas des manipulations manifestes) ?

• Contenus et objectifs disciplinaires

Statistiques et représentations de données ; calculs ; proportionnalité et pourcentages.

Scénario

Des diaporamas de situations à questions ouvertes sont projetées lors de séances différentes, quasi-successives sur un intervalle de 3 semaines, pour développer des automatismes.

Le travail individuel pour chaque situation est assez court. Les réponses sont écrites sur une fiche dédiée qui est distribuée au début de chaque exercice.

Puis les élèves engagent un débat oral, plus ou moins dirigé par le professeur ou par un ou plusieurs élèves.

Un bilan sur les utilisations des mathématiques et les erreurs que l’on peut rencontrer est ensuite établi collectivement, oralement ou au tableau, et copié par les élèves. Le professeur met en lumière des biais cognitifs et la nécessité de se méfier dans certains cas, d’activer d’autres réflexes (vérifications rapides par des calculs, lectures plus attentives de diagrammes).

Les compétences

Compétences du CRCN-édu  mobilisées par l’enseignant

Domaine 1 : DÉVELOPPEMENT PROFESSIONNEL

• 1.5 Adopter une posture ouverte, critique et réflexive.

Domaine 2 : GESTION DES RESSOURCES NUMÉRIQUES Sélectionner, créer et gérer des ressources

• 2.1 Sélectionner des ressources.

• 2.2 Concevoir des ressources.

Domaine 3 : ENSEIGNEMENT-APPRENTISSAGE AVEC ET PAR LE NUMERIQUE

• 3.1 Concevoir.

• 3.2 Mettre en œuvre

Déroulement de la séance

Trois séries ont été expérimentées dans deux classes de 3ème.

• Déroulés et évolution des séances

La méthode de travail, répétant un type d’exercice avec des situations similaires, a été annoncée dès le début. A l’issue de la première série, l’enseignante a expliqué aux élèves que l’objectif de ce travail était de développer leur esprit critique face à des visuels qu’ils peuvent rencontrés dans la vie de tous les jours. Les élèves ont eu beaucoup de difficultés à formuler ce qu’ils ont effectivement travaillé : ce travail de prise de recul, en cherchant le point commun aux situations étudiées, et en même temps de formulation, leur a été difficile.

Une fois la correction faite, la partie « ce que je retiens » a été complétée en autonomie par les élèves. Le bilan a été parfois écrit, parfois oral, il est élaboré avec et pour la classe.

Fichier du diaporama 1 des questions-flash en version pdf.

Série 1 : elle a nécessité beaucoup plus de temps que prévu (45 à 50 min selon la classe) pour que les élèves entrent dans la tâche et fournissent des réponses à peu près adaptées. Les situations ont été données une à une. La correction a été faite après chaque diapo de la série afin que les élèves comprennent bien les attentes. Un soin particulier a été apporté pour expliciter le type de réponses attendues, comment tourner les phrases.. Les erreurs mathématiques ont été identifiées assez facilement.

Fichier du diaporama 2 des questions-flash en version pdf.

Série 2 : elle a été donnée deux semaines environ après la première. Plusieurs élèves n’ont pas repris cette tâche avec plaisir, manifestant leur mécontentement. La seconde classe qui a fait cet exercice, à la fin d’une séance, n’a pas réussi à atteindre la troisième et dernière situation alors que le temps de travail était le même.

Fichier du diaporama 3 des questions-flash en version pdf.

Série 3 : Cette série a été particulièrement attractive, les élèves sont rentrés facilement dans l’activité. Les réticences ont été bien moindres en début de travail, les écrits ont été plus fournis, les réactions plus naturelles et variées lors des débats.

La situation 3 (capture d’écran d’un bulletin météorologique de la télévision espagnole) a été mise en scène lors de la correction avec un élève qui mimait la présentatrice. Cette image est très intéressante pour faire ressortir des biais cognitifs variés. En particulier, les deux premières courbes de températures comportent des erreurs alors que la troisième est correctement représentée. Les élèves ont conclu, un peu hâtivement, que la dernière courbe comportait elle aussi des erreurs. La situation 4 est, elle aussi, pertinente. En effet le diagramme est facile à comprendre (seulement trois catégories sont représentées). La proportion de 48% est facilement vérifiable. Le temps consacré à l’interprétation a donc été plus important.

• Productions d’élèves et analyses

Exemples d’écrit où l’élève a bien compris ce qui était attendu dès la série 1 :

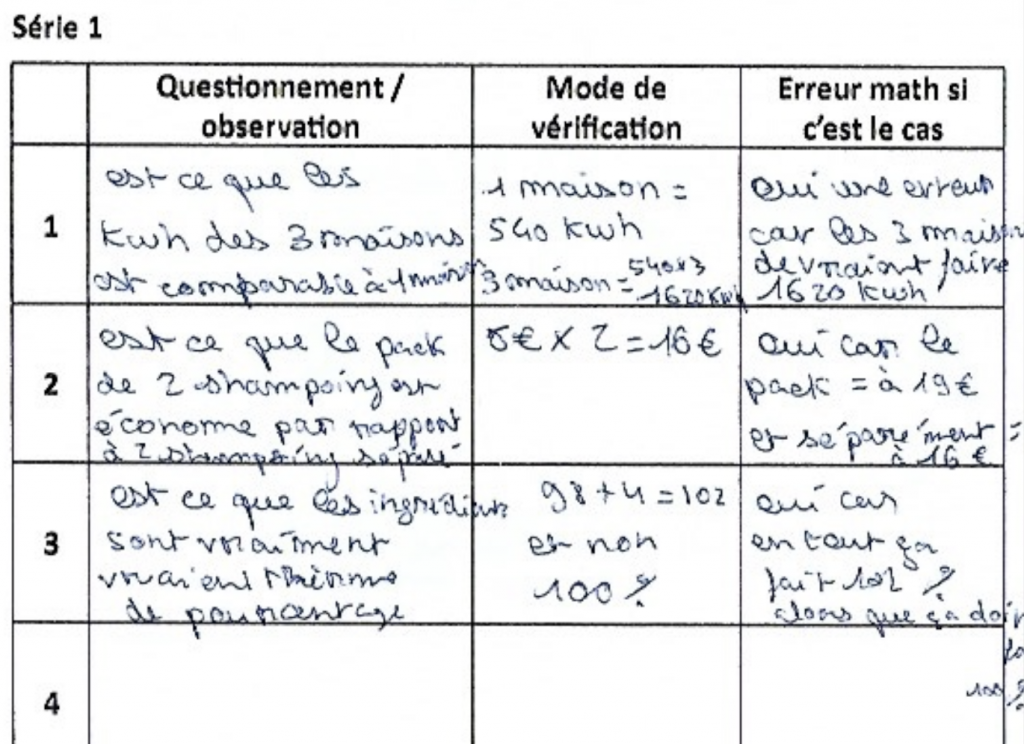
Les élèves se sentent concernés par les situations proposées, mais ils s’attachent beaucoup au contexte et peu à l’objectif d’apprentissage. Ils généralisent facilement les observations réalisées.

Exemple d’élève qui prend un peu de recul par rapport à la tâche et fait le lien entre le travail scolaire et la vie courante :

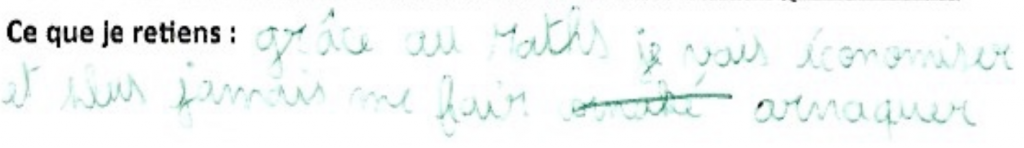
Lors de l’exercice de la série 3, les élèves ont bien progressé dans leur analyse.  Ils semblent avoir développé leur esprit critique au service de la vie quotidienne, en lien avec les mathématiques. Les élèves qui étaient habituellement en grandes difficultés scolaires ont pu eux aussi progresser.

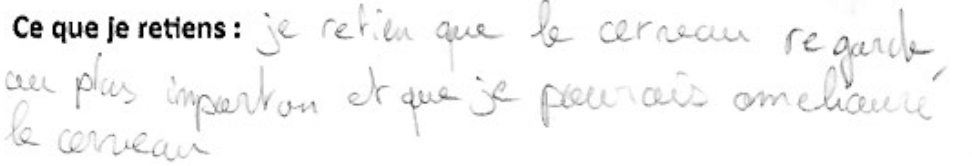
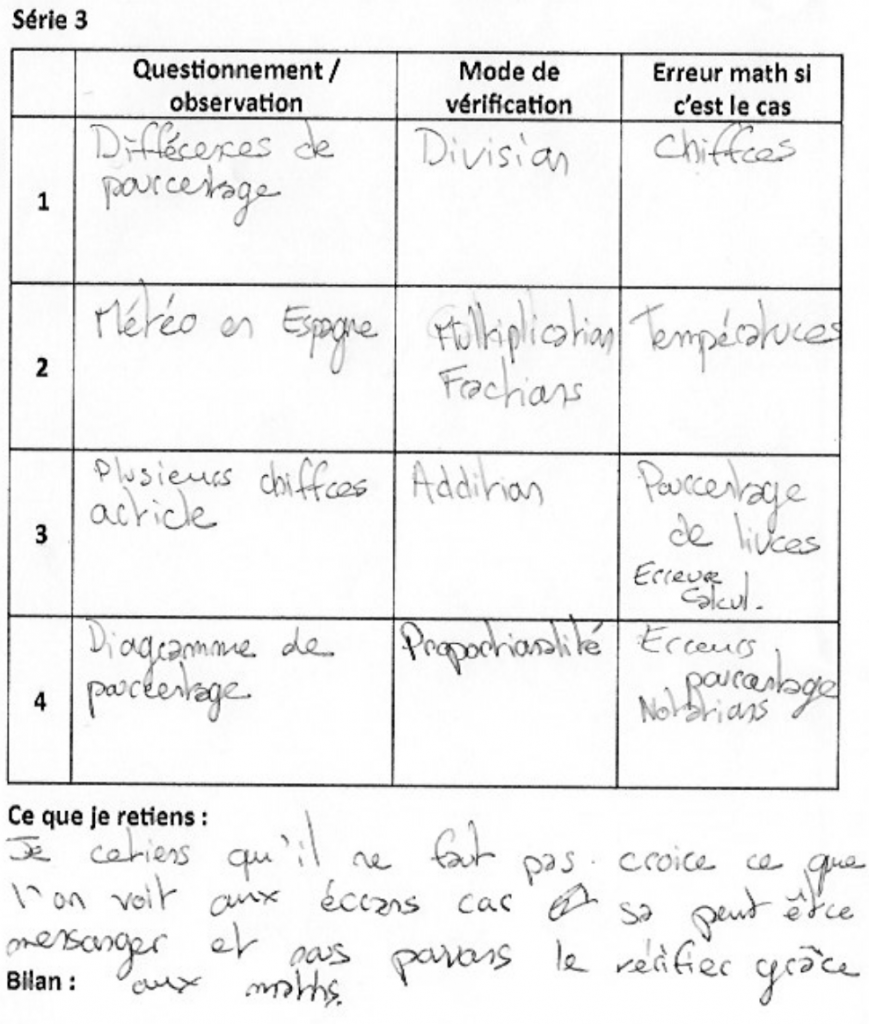
Premier point de vigilance : plusieurs élèves se sont placés en juges des autres, auteurs d’erreurs, et cela paraît assez excessif.

Autre point de vigilance : un autre élève semble avoir développé une crainte excessive de se trouver face à une erreur (de bonne foi ou non) qui lui ferait perdre le contrôle, et il semble inquiet de devoir sans arrêt se méfier :

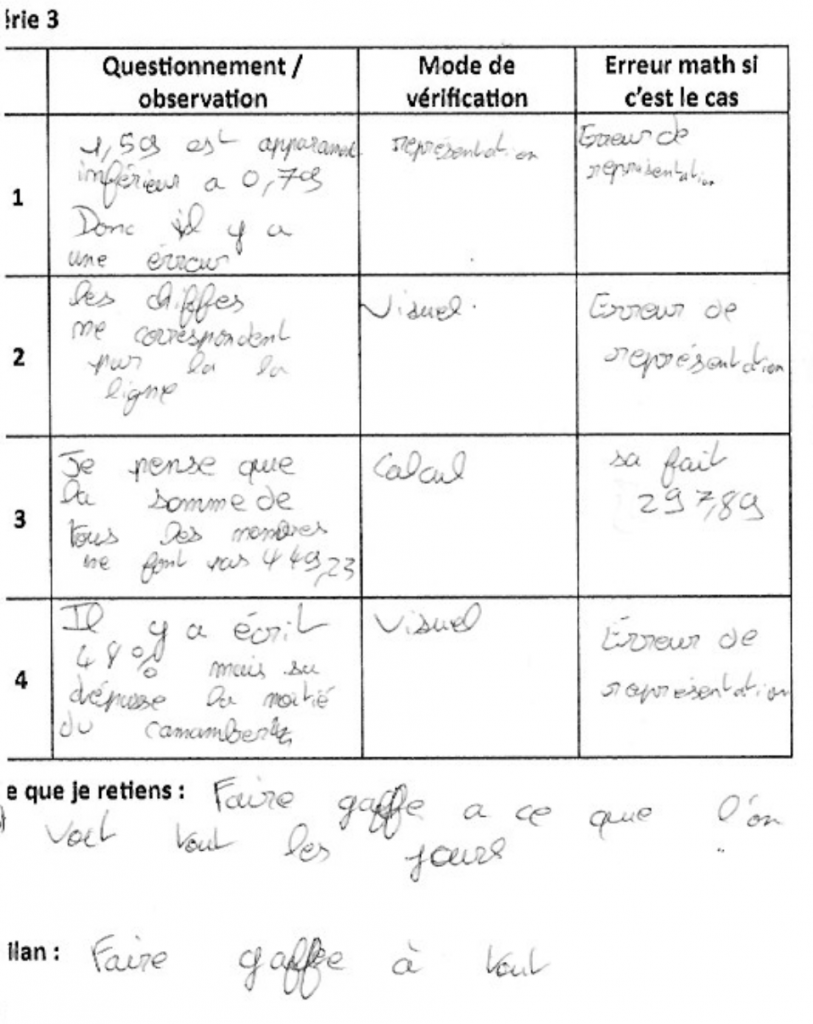
• Réussite et obstacles

Réussites :

• La plupart des situations sont faciles à prendre en main par les élèves.
• La répétition de la tâche sur plusieurs séances (plusieurs séries) et avec des exemples simples ou assez simples, permet de rendre les élèves plus efficaces dans le repérage des erreurs, dans les interprétations et dans la compréhension des objectifs d’apprentissage.
• Parmi les élèves les plus en difficulté, plusieurs ont prouvé dans leur bilan de la série 3 qu’ils avaient compris les situations et surtout atteint l’objectif de la tâche.
• Les biais cognitifs : le biais de cadrage et le biais de confirmation (tendance à être influencé par la manière dont une situation est présentée) sont rencontrés plusieurs fois et mis assez facilement en exergue.
• La situation 3 de la série 3 a permis de rencontrer le biais de halo (ou de généralisation abusive).

Obstacles :

• Le premier obstacle est la compréhension des consignes. Les élèves ont presque tous mis du temps à comprendre ce qui était attendu d’eux dans les fiches-réponses, malgré les reformulations des consignes et la multiplication des exemples. L’exemple 1 de la séance 1 a peut-être été trop complexe : un exemple plus simple, où l’erreur serait plus facile à repérer et où le contexte serait plus familier, serait préférable.
• Le principal obstacle est la difficulté des élèves à prendre de la hauteur par rapport à la tâche, à synthétiser ce qui est travaillé réellement, à faire de la métacognition. Ils restent très attachés dans leurs bilans (partie « ce que je retiens ») aux situations réelles. Ces élèves-là, qui peuvent avoir des facilités en mathématiques, ne retiennent pas que les mathématiques peuvent leur permettre de faire preuve d’esprit critique dans des situations de la vie courante. Les émotions prennent le dessus et ils formulent surtout que « il faut faire attention aux arnaques », « on se fait avoir » ou « c’est des menteurs ». Un élève en grande difficulté est même resté focalisé sur une seule situation et cite la chaîne de télévision française d’où une erreur a été extraite. La gestion des sources n’est donc pas facile à faire par le professeur. Il devra rester vigilant sur le choix des sources utilisées, et proposer un panel le plus riche et varié possible.
• Pour un élève très efficace généralement dans les tâches scolaires, il ressort à la fin de la série 3 que « on doit faire gaffe à ce que l’on voit tous les jours, […] faire gaffe à tout », ce qui prouve qu’il a généralisé les exemples montrés et qu’il est dans une situation très inconfortable.

Bilan final et perspectives

L’impression finale de cette expérimentation est positive. Il serait cependant souhaitable de mettre en œuvre davantage d’exercices de ce type afin que la tâche soit plus efficace, une fois que les consignes et objectifs sont compris et que la fiche-réponse est mieux prise en main. Après deux exercices semblables, sur des exemples proches mais pas forcément nombreux, on pourrait proposer des situations où il n’y aurait pas d’erreur mathématique afin de mieux exercer les réflexes. Si tous les exemples comportent une erreur, le cerveau s’adapte à l’exercice mais il pourrait perdre du temps dans la vie courante où les erreurs ne sont pas si fréquentes.

Le temps de travail plus long que prévu sur les premières séries n’a pas permis d’expliquer aux élèves ce que sont les biais cognitifs, même rapidement et oralement, ni quels étaient ceux qui semblaient à l’œuvre dans leurs différentes réponses et réactions. Cette explication aurait pu leur être utile afin de comprendre le pourquoi de leurs réponses et de leurs réactions.

Le tableau de la fiche-réponse pourrait aussi être simplifié, avec des formulations du type “Y a-t-il une erreur mathématique ? Si oui, laquelle ? Pouvez-vous la corriger ?”. Les consignes qui suivent le tableau (espace pour dire ce que l’on retient et pour écrire un bilan) peuvent être conservées.

Ressources : fichiers à projeter et fiche-réponses

Fiches-réponses à télécharger.