Objectif :
Utiliser différentes méthodes pour démontrer une égalité.
Méthode 1 :
On transforme par étapes successives un membre de l’égalité à établir pour obtenir le second.
- Prouver par cette méthode que
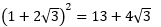
- Prouver que, quel que soit le nombre réel x,
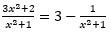
Méthode 2 :
On transforme chaque membre de l’égalité pour montrer qu’ils sont égaux à un même réel.
Démontrer par cette méthode que, pour tout réel x,
![]()
Applications :
- Démontrer que la différence des carrés de deux entiers consécutifs est égale à la somme de ces deux entiers.
- Démontrer que tout nombre impair est la différence des carrés de deux nombres consécutifs.
- Lorsque l’on augmente de 1 le produit de quatre nombres entiers consécutifs, obtient-on un carré parfait ?
Fiche élève Démontrer une égalité word
Fiche élève Démontrer une égalité pdf


