La formation au raisonnement et l’initiation à la démonstration sont toujours des objectifs du cycle 4, comme dans les programmes précédents. Mais l’élève de cycle 3 raisonne aussi et le professeur l’aide à mettre en mots, oralement, les étapes de ses raisonnements, les sens déductifs et les quantificateurs. Lui-même doit se montrer très précis, expliciter le sens logique, notamment en employant la locution « si … alors .. » dans chaque énoncé de propriété, à l’oral comme à l’écrit. Il indique les liens déductifs, démontre dès que possible pour montrer aux élèves que les résultats mathématiques ne sont pas de son invention mais qu’ils sont universels, qu’ils ont une histoire. Les mathématiques sont basées sur des axiomes mais se construisent par raisonnement logique étayé. Cette formation des élèves est importante au-delà du cours de mathématiques parce qu’elle donne du sens aux notions à retenir et développe leur esprit critique.
Raisonner et communiquer
Les six compétences mathématiques sont toujours au programme du cycle 3 de 2025. Ainsi, le professeur s’attachera à distinguer en formation comme en évaluation, le raisonnement et la communication du raisonnement. De plus, il n’aura que très peu d’exigence sur la communication écrite en 6e. L’enseignement sera donc basé sur beaucoup d’oral et d’efforts de reformulation que l’on demandera aux élèves.
Pour bien raisonner, on apprendra aux élèves à repérer les informations (texte, codages, résultats des étapes précédentes) ; à distinguer ces informations de ce à quoi ressemble la figure et qui ne pourrait donner lieu qu’à des conjectures ; à distinguer ce que l’on sait et ce que l’on cherche à prouver ; à faire le lien entre ces deux types d’éléments en passant par des définitions ou propriétés connues ; à ne pas s’appuyer sur un ou quelques exemples pour conclure qu’un résultat est toujours vrai.
Raisonnement utilisant la distance d’un point à un autre : raisonner pour construire
Le fascicule Résolution de problèmes au collège mentionne un type d’exercices important pour les apprentissages en géométrie : des exercices qui font « raisonner pour construire », c’est-à-dire dans lesquels la consigne est simplement de construire une figure dont on donne suffisamment d’éléments, mais qui ne pourra pas être mise en œuvre sans avoir au préalable conduit un petit raisonnement. Celui-ci doit s’appuyer sur un schéma codé que l’on impose de faire à l’élève.
Si l’on demande de construire un triangle IJK rectangle en J tel que JK = 5 cm et IK = 6,5 cm, en utilisant les données dans l’ordre, les élèves n’auront pas de difficulté particulière à tracer le segment [JK], puis à construire la perpendiculaire passant par J et ils tenteront de faire tourner leur règle avec le 0 placé sur K jusqu’à ce que la graduation de 6,5 cm coïncide avec la perpendiculaire. Le professeur et eux constateront que la construction peut être tout à fait acceptable en comparant avec un calque, mais qu’il n’y a pas de trait de construction. C’est le professeur qui invalide la méthode en mentionnant que les usages de la règle qui ont été établis ne sont pas respectés (voir par exemple le fascicule sur la restauration de figures de l’IREM de Bordeaux). Il lui faut alors faire étudier le schéma codé à la classe en le faisant dessiner au tableau. Il fera formuler qu’à la troisième étape, on cherche à placer un point sur la perpendiculaire qui soit aussi à 6,5 cm de K, ce qui est reformulé peu à peu en « le point I est le point d’intersection de la perpendiculaire et du cercle de centre K et de rayon 6,5 cm ». Aucun texte ne sera écrit pour retranscrire ce raisonnement, mais, tant que c’est nécessaire pour ce type d’exercice, le professeur fera noter le programme de construction qui mentionnera les outils utilisés et explicitera que les traits de construction doivent être conservés mais tracés fins pour ne pas surcharger la figure.

Un autre exemple (dans le rectangle mais se ramenant à un triangle rectangle comme dans ce qui est proposé ci-dessus) est donné page 153 du fascicule Résolution de problèmes au collège.
Raisonnement utilisant la somme des angles d’un triangle : raisonner pour construire
Par exemple, après avoir demandé de construire, à la règle et au rapporteur, un triangle isocèle dont on donne la mesure de la base et celle d’un angle à la base, on propose à l’exercice suivant :
« Construire le triangle ABC isocèle en A tel que : BC = 4 cm et = 50°. » Les élèves qui vont trop vite verront leur erreur avec un calque d’auto-correction. Le professeur les oriente alors en leur faisant constater que, soit ils n’ont pas fait le schéma codé demandé en premier, soit il ne correspond pas à la description de la figure donnée dans l’énoncé.
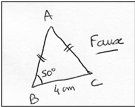
Voir article La géométrie perceptive en 6e (lien)
Ce schéma codé montre à l’élève que, même s’il peut tracer [BC], la base du triangle, il ne peut pas placer son rapporteur pour mesurer l’angle .
Ici aussi, le schéma codé est analysé et permet le raisonnement utilisant la propriété de la somme des angles d’un triangle.

Le raisonnement est une partie indispensable de la réponse mais son écriture est complexe en 6e. Il est une étape incontournable pour mener à bien une construction géométrique, activité abordable facilement et souvent motivante pour des élèves de 6e. L’envie de parvenir à finir la construction motive l’effort du raisonnement.
Remarque : ce type d’exercice doit être conduit plusieurs fois en classe mais peut ensuite être demandé en devoir en temps libre évalué. En effet, même si quelqu’un ou une IA aide l’élève à raisonner, on peut attendre une trace simple de ce raisonnement ou même simplement les traits de construction qui prouveront que le raisonnement a été fait en amont. Et la construction ne peut pas être faite par une IA …
La nécessité d’une preuve : le point de concours des médiatrices du triangle
Le fascicule Résolution de problèmes au collège reprend page 138 une activité proposée par Guy Brousseau et qui peut maintenant être conduite en 6e. Il s’agit de l’activité de construction dite du « co-triangle », et intitulée dans le fascicule « figure trompeuse ». Elle s’utile en classe après avoir enseigné la médiatrice d’un triangle et dans le but d’établir que les trois médiatrices d’un triangle sont concourantes.
Tout d’abord, le professeur montre une figure qu’il a tracée sur une feuille A3 :

Il demande aux élèves de l’aider à la décrire : il s’agit d’un triangle (placé tout en haut de la feuille) et des médiatrices de ses trois côtés. Celles-ci se coupent deux à deux en formant un petit triangle que le professeur appellera le « co-triangle ». Le triangle a un grand angle obtus (« tourné vers le bas ») mais il n’est pas nécessaire de le faire remarquer à ce stade. Le grand format, le tracé avec la règle et l’équerre et les médiatrices qui se coupent loin du triangle en raison de l’angle obtus ont accentué les erreurs de tracé et mené à ne pas réussir à construire le point de concours. Le professeur peut avoir forcé un peu l’erreur mais il ne le mentionne surtout pas. La consigne est alors : « je vous demande de tracer un triangle, celui que vous voudrez, et de construire les médiatrices de ses côtés afin d’obtenir le co-triangle le plus grand possible ».
Or, au contraire, plus les élèves s’appliquent, et plus le co-triangle disparaît … Le raisonnement est alors la seule solution pour comprendre ce phénomène.
Une fois la preuve de la concourance des médiatrices établie, le professeur devra expliquer pourquoi il avait une erreur manifeste mais normale car les tracés sont vite imprécis en géométrie. Il fait ainsi apparaître que l’on doit malgré tout s’appliquer le plus possible en construction à la main, mais que seul le raisonnement s’appuyant sur des propriétés déjà établies permet d’être sûr d’un autre résultat.
Pendant tout le reste de l’année scolaire, l’activité du co-triangle devient la référence partagée lorsque les élèves concluent trop vite ou rechignent à établir un raisonnement rigoureux.
Attention, la preuve de l’existence du point de concours des médiatrices est menée par le professeur avec les élèves, elle donne lieu à des formulations précises, rigoureuses, et variées, mais elle est formalisée le moins possible à l’écrit.

L’existence du point d’intersection des deux premières médiatrices n’a pas à être démontrée en 6e, même si on peut mentionner pourquoi il existe.
Conclusion
« Le passage de la géométrie perceptive à la géométrie du raisonnement est délicat et doit être accompagné de situations-problèmes qui illustrent la force du raisonnement. » (Fascicule Résolution de problèmes au collège page 156).
Les raisonnements et preuves doivent s’appuyer sur des énoncés, clairs et distincts, de définitions (voir document Tableaux définitions et preuves.pdf) et propriétés, que les élèves doivent mémoriser, notamment grâce à leur répétition dans le temps, lors d’exercices de géométrie ou de questions-flash. Le professeur en mène seul (ou avec les élèves) plusieurs, puis il peut leur apprendre à les appliquer dans des exercices de calcul.


