Voici une série d´énigmes pour le lycée. Celles en anglais, ont été sélectionnées et rédigées par des élèves du lycée Victor Louis de Talence (33), celles en espagnol par le lycée De Borda de Dax (40). D’autres énigmes proposées en français sont issues de divers concours (Olympiades, Mathématiques sans frontières…).
Elles sont annotées selon deux niveaux de difficulté :
- niveau 1: pour tous
- niveau 2: davantage de méthodes s´imposent
Les solutions de toutes ces énigmes seront diffusées sur ce site à la fin de la semaine des mathématiques.
Énigme 1 : (Niveau 1) A boat and a lifeboat
A boat with 15 people on board is going to sink in about 20 minutes. There is just one lifeboat which can contain 5 people at once.
There are sharks around and it takes 9 minutes to go to the island and back to the boat.
How many people can be rescued?
Énigme 2 : (Niveau 1) A synchronised swimming show
A leading organizer is auditioning today no more than 20 people for a show of synchronised swimming.
5 people don’t know how to swim. Among the people who know how to swim, a third are women and a quarter are less than 25 years old.
How many people went to the audition?
Énigme 3: (Niveau 1)
Santa Clause crosses in his sledge the circumference of the Earth at 100 meters above the ground. Doing that, he has travelled 40 000 kilometres. If he achieved the same travel at 500 meters higher, how many more kilometres than during his first travel, he will travel? The result must be rounded to the tenth.
Énigme 4: (Niveau 1)
Bryan and Christina are running errands for Christmas presents.
In the first shop, they spend half of their money and 10$.
In the second shop, they spend half of their left-over money and 10$.
In the third shop, they spend half of their left-over money.
In the last shop, they spend the final 10$.
How much did they have at the beginning of this busy day?
Énigme 5: (Niveau 1) How old are you, Peter?
At a tea party, Elizabeth and Mary speak about the age of Elizabeth’s husband, Peter. Elizabeth, a mathematics lover, gives Mary a riddle to find out the age of Peter:
« To find the age of my husband, you just have to reverse the order of the number of my age. Peter is older than me and our difference in age is exactly equal to the eleventh of the sum of our age. How old is Peter? »
Of course, you can’t ask Peter, because it’s not elegant to request the age of somebody in our English society…
Énigme 6: (Niveau 1) THE TWO STRANDS OF HAIR
You have strands of hair, a pair of scissors and a lighter. It takes 1 hour to burn one strand of hair; even if consumption is irregular. You don’t have any watch or anything else to value the time…
How can you calculate if 45 minutes have passed?
Énigme 7: (Niveau 1)
Three people rent a room at $30. They pay $10 each and go up to the room. The owner realized he charged too much because the room was only supposed to be $25. He sends the bell hop up with the $5. Each of them keeps $1 and they give the bellhop $2 as they can’t share it. So now each person has paid $9 for the room (total $27) and the bell hop has $2… Where is the other $1?
Énigme 8: (Niveau 1)
Imagine a bridge and a family.
In this family, there is the grand-mother, who takes 10 min to cross the bridge, the mother, who takes 5 min, the father, who takes 2 min, and the son, the fastest who takes 1 min. The family needs to cross the bridge because a tiger appears in 17 min. It’s the night, so, the family needs a lamp to cross the bridge. There is only one lamp, and the members of the family can only cross 2 by 2.
Help them to succeed.
Remember! To cross the bridge, you NEED the lamp.
Time considered is the slower of the two.
Example: if the father crosses the bridge with the mother, they take 5 min to cross it.
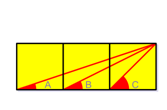
Énigme 9: (Niveau 1)
Using only elementary geometry (not even trigonometry), find out what the sum of the angles A + B + C is.
A + B + C =?
Énigme 10: (Niveau 2)
A man is driving his car to the office at 20 miles/hr.
When arriving at the office, he realizes that it´s a day off (New Year´s Day!!!), so, he immediately decides to go back home at a speed of 30 miles/hr.
What will be the average speed of his entire useless journey?
Énigme 11: (Niveau 2) Fair-haired and red-haired persons
In this country, which you will not find on any map, it happens that fair-haired persons always lie and that red-haired persons always tell the truth.
Three inhabitants of this country are gathered in a room. They wear hats which hide their hair.
The first one is saying: “I am …”, but you can’t understand the end of his sentence.
The second is saying, “He said he is red-haired.”
You’re asking the third by pointing the first with the finger: “Did he tell the truth?”. The third answer is no. You’re pointing then the second: “Is he red-haired?”. He is also answering that he isn’t.
What is the colour of their hair?
Énigme 12: (Niveau 2)
Imagine you have 9 marbles and a balance scale. You know that the marbles are all the same weight except for one marble, which is heavier.
How can you work out which one it is with only two measurements on the scale?
Énigme 13: (Niveau 2)
A Bedouin died in the desert. He had 17 camels and 3 children.
After his death he gave half of the camels to his first child, the third to the second and 1/9 to the last one. The children who cannot cut camels into parts, decided to visit the wise old man of the desert to know how to manage.
How could the wise old man help them?
Énigme 14 : (Niveau 1) Three interrupters enigma
In a room without windows there is a light. At the exterior of the room there are three interrupters on position “off”. You can go just once into the room. What should you do to know which interrupter is the right one?
Énigme 14: (Niveau 1) Bombilla encendida… o no
Por delante, tienes 3 interruptores. Uno de ellos (nadie sabe cuál es) enciende una bombilla en una casa situada a 100 metros de distancia. Disponiendo solo de una ida y vuelta hacia la casa, ¿Qué hay que hacer para saber cuál de los tres enciende la bombilla?
Énigme 15 : (Niveau 1)
Buscamos un número de 6 dígitos que incluye:
- El primero y el último digito son los mismos.
- Si se multiplica el primer número por 2 produce un número de dos cifras.
- Dichas cifras representan el segundo y el tercer digito.
- El ultimo digito multiplicado por 3 da un numero de 2 dígitos.
- Estos dos dígitos son el cuarto y el quinto.
- La suma de los 6 dígitos es 22.
¿Cual es este nombre?
Énigme 16: (Niveau 1) El enigma de Einstein
En un barrio, hay 5 casas de color diferente. En cada casa, vive una persona de nacionalidad diferente. Cada persona fuma un tipo de cigarrillo diferente, bebe una bebida diferente y tiene una mascota diferente.
¿Con los elementos siguientes, puede decir quien tiene un pez?
- El inglés vive en la casa roja.
- El español tiene un perro.
- El francés bebe té.
- La casa verde está situada a la izquierda de la casa blanca.
- En la casa verde, se bebe café.
- El fumador de Pall Mall tiene un pájaro.
- En la casa del medio se bebe leche.
- En la casa amarilla se fuma Dunhills.
- El italiano vive en la primera casa.
- El fumador de Rothmann tiene un vecino que tiene un gato.
- El que tiene un caballo, tiene un vecino que fuma Dunhills.
- El fumador de Phillip Morris bebe cervezas.
- El italiano es vecino con la casa azul.
- El alemán fuma Malboro.
- El fumador de Rothmann tiene un vecino que bebe agua.
Énigme 17 : (Niveau 1) Dates surprenantes
On peut écrire les dates sous la forme JJ.MM.AAAA. Par exemple, le 17 mars 2017 s´écrit 17.03.2017.
On dit qu´une date est surprenante si, écrite sous cette forme, ses 8 chiffres sont différents.
- Quelle est la prochaine date surprenante?
- Quelle est la date surprenante passée la plus proche ? (D´après le Concours Kangourou)
Énigme 18 : (Niveau 1)
« Cette tombe renferme Diophante. Ô merveille, elle dit mathématiquement combien il a vécu. Dieu lui accorda un sixième de sa vie pour son enfance ; il ajouta un douzième pour que ses joues se couvrissent du duvet des adolescents ; en outre, pendant un septième de sa vie, il fit brûler pour lui le flambeau d´hymen, et après cinq ans de mariage il lui donna un fils, hélas ! unique et malheureux enfant, auquel la Parque ne permit de voir que la moitié de la vie de son père. Pendant quatre ans encore, consolant sa douleur par l´étude des chiffres, il atteignit enfin le terme de sa vie. »
Quel âge avait Diophante au terme de sa vie ? (Enigme de Métrodore, 5è siècle)
Énigme 19 : (Niveau 1)
Si dans un ouvrage, on augmente chaque page de 3 lignes et chaque ligne de 4 lettres, la page contiendra 228 lettres de plus. Mais si l´on diminue la page de 2 lignes et la ligne de 3 lettres, chaque page contiendra 147 lettres de moins.
Quel est le nombre de lignes de chaque page et le nombre e lettres de chaque ligne ? (Élèments d´algèbre par G. B. J. Raingo, Mons, Belgique, 1842)
Énigme 20 : (Niveau 1)
Un nombre divzar est un nombre entier positif n dont la somme de tous ses diviseurs (sauf lui-même) est plus grande que n mais dont aucune somme de certains de ses diviseurs n´est égale à n. Quel est le plus petit nombre divzar ? (Rallye mathématique d´Aquitaine)
Énigme 21 : (Niveau 1)
Deux parallélépipèdes sont tels que les longueurs en centimètres de leurs arêtes sont des nombres entiers. L´un est un cube, l´autre a une base carrée et sa hauteur mesure 1 cm. Si les deux parallélépipèdes ont le même volume et que celui-ci est inférieure à 2017 , quel est leur plus grand volume possible ?
Énigme 22 : (Niveau 1)
Un sac contient des billes rouges, blanches et bleues en très grande quantité.
Chaque élève de mon école prend au hasard trois billes. Trouver le nombre minimum d´élèves nécessaires pour être sûr qu´il y ait deux élèves à avoir pris la même combinaison de billes, c´est-à-dire le même nombre de billes de chaque couleur.
Énigme 23 : Niveau 2 (D´après un sujet des Olympiades)
On s´intéresse à l’arbre généalogique de Benjamin. On décide de numéroter ses ascendants. Le début de cette numérotation est représenté par le schéma ci-dessous :
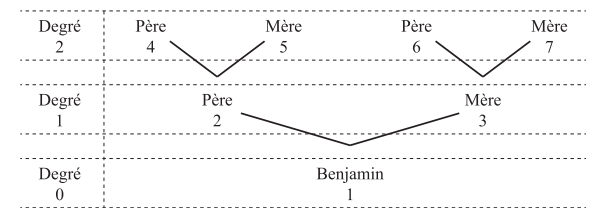
- Compléter la ligne de degré 3.
- On suppose que tous les ascendants au degré n sont des personnes différentes. Donner, sans justifier, le nombre d’ascendants au degré 4 puis au degré n.
- On s´intéresse à l´ascendant numéro 712.
a) S’agit-il d’un homme ou d’une femme?
b) Quel est le degré de cet ascendant?
c) S’agit-il d’un ascendant du côté du grand-père paternel de Benjamin, de sa grand-mère paternelle, de son grand-père maternel ou de sa grand-mère maternelle?
d) Combien compte-t-on de femmes sur le chemin de l’arbre qui relie Benjamin à cet ascendant?
Énigme 24 : (Niveau 2) (D´après un sujet des OFM)
On dispose de 100 ampoules, numérotées de 1 à 100, chacune pouvant être soit allumée soit éteinte. Ces ampoules sont reliées à trois commutateurs A, B et C.
En appuyant sur A, on change l’état de toutes les ampoules : celles qui étaient allumées s’éteignent, et celles qui étaient éteintes s’allument.
En appuyant sur B, on ne change l’état que des ampoules de numéros impairs.
En appuyant sur C, on ne change l’état que des ampoules de numéros de la forme 3n +1.
Au début de la soirée, toutes les ampoules étaient allumées. Mais, au cours de la fête et emporté par son enthousiasme, Igor a appuyé au total 1000 fois, de façon aléatoire, sur les commutateurs. Il se trouve qu’alors les ampoules portant les numéros 95 et 96 sont éteintes.
Combien d’ampoules sont encore allumées?


 s
s
